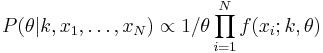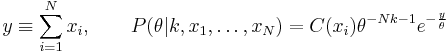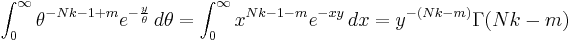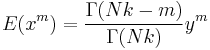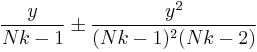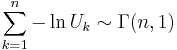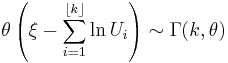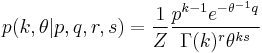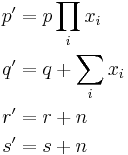Gamma distribution
| Probability density function |
|
| Cumulative distribution function |
|
| Parameters | |
|---|---|
| Support | 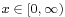 |
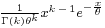 |
|
| CDF | 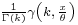 |
| Mean | 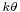 |
| Median | No simple closed form |
| Mode | 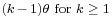 |
| Variance | 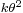 |
| Skewness | 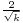 |
| Ex. kurtosis | 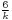 |
| Entropy | ![\scriptstyle \begin{align}
\scriptstyle k &\scriptstyle \,%2B\, \ln\theta \,%2B\, \ln[\Gamma(k)]\\
\scriptstyle &\scriptstyle \,%2B\, (1 \,-\, k)\psi(k)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/c9003f3a6310f3bf3cc6f09a208ec6f2.png) |
| MGF | 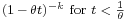 |
| CF | 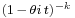 |
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. It has a scale parameter θ and a shape parameter k. If k is an integer, then the distribution represents an Erlang distribution; i.e., the sum of k independent exponentially distributed random variables, each of which has a mean of θ (which is equivalent to a rate parameter of θ−1) .
The gamma distribution is frequently a probability model for waiting times; for instance, in life testing, the waiting time until death is a random variable that is frequently modeled with a gamma distribution.[1] It is the maximum entropy probability distribution for a random variate X for which 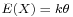 is fixed and greater than zero, and
is fixed and greater than zero, and ![\scriptstyle E[\ln(X)] \;=\; \psi(k) \,%2B\, \ln(\theta)](/2012-wikipedia_en_all_nopic_01_2012/I/0deb4a4a217ff745003b35c06a7ea2f5.png) is fixed (
is fixed (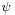 is the digamma function).[2]
is the digamma function).[2]
Contents |
Characterization
A random variable X that is gamma-distributed with scale θ and shape k is denoted
Probability density function
The probability density function of the gamma distribution can be expressed in terms of the gamma function parameterized in terms of a shape parameter k and scale parameter θ. Both k and θ will be positive values.
The equation defining the probability density function of a gamma-distributed random variable x is
(This parameterization is used in the infobox and the plots.)
Alternatively, the gamma distribution can be parameterized in terms of a shape parameter α = k and an inverse scale parameter β = 1⁄θ, called a rate parameter:
If α is a positive integer, then
Both parametrizations are common because either can be more convenient depending on the situation.
Cumulative distribution function
The cumulative distribution function is the regularized gamma function:
where 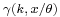 is the lower incomplete gamma function.
is the lower incomplete gamma function.
It can also be expressed as follows, if k is a positive integer (i.e., the distribution is an Erlang distribution):[3]
Properties
Median calculation
Unlike the mode and the mean which have readily calculable formulas based on the parameters, the median does not have an easy closed form equation. The median for this distribution is defined as the constant x0 such that
The ease of this calculation is dependent on the alpha parameter. This is best achieved by a computer since the calculations can quickly grow out of control.
Summation
If Xi has a Γ(ki, θ) distribution for i = 1, 2, ..., N (i.e., all distributions have the same scale parameter θ), then
provided all Xi' are independent.
The gamma distribution exhibits infinite divisibility.
Scaling
If
then for any α > 0,
Exponential family
The Gamma distribution is a two-parameter exponential family with natural parameters k − 1 and −1⁄θ, and natural statistics X and ln(X).
Information entropy
The information entropy is given by
where ψ(k) is the digamma function.
One can also show that (if we use the shape parameter k and the inverse scale parameter β),
Or alternatively, using the scale parameter θ,
Kullback–Leibler divergence
The directed Kullback–Leibler divergence between 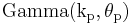 ('true' distribution) and
('true' distribution) and 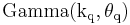 ('approximating' distribution) is given by[4]
('approximating' distribution) is given by[4]
Laplace transform
The Laplace transform of the gamma PDF is
Parameter estimation
Maximum likelihood estimation
The likelihood function for N iid observations (x1, ..., xN) is
from which we calculate the log-likelihood function
Finding the maximum with respect to θ by taking the derivative and setting it equal to zero yields the maximum likelihood estimator of the θ parameter:
Substituting this into the log-likelihood function gives
Finding the maximum with respect to k by taking the derivative and setting it equal to zero yields
where
is the digamma function.
There is no closed-form solution for k. The function is numerically very well behaved, so if a numerical solution is desired, it can be found using, for example, Newton's method. An initial value of k can be found either using the method of moments, or using the approximation
If we let
then k is approximately
which is within 1.5% of the correct value. An explicit form for the Newton-Raphson update of this initial guess is given by Choi and Wette (1969) as the following expression:
where 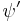 denotes the trigamma function (the derivative of the digamma function).
denotes the trigamma function (the derivative of the digamma function).
The digamma and trigamma functions can be difficult to calculate with high precision. However, approximations known to be good to several significant figures can be computed using the following approximation formulae:
and
For details, see Choi and Wette (1969).
Bayesian minimum mean-squared error
With known k and unknown  , the posterior PDF for theta (using the standard scale-invariant prior for
, the posterior PDF for theta (using the standard scale-invariant prior for  ) is
) is
Denoting
Integration over θ can be carried out using a change of variables, revealing that 1⁄θ is gamma-distributed with parameters 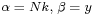 .
.
The moments can be computed by taking the ratio (m by m = 0)
which shows that the mean ± standard deviation estimate of the posterior distribution for theta is
Generating gamma-distributed random variables
Given the scaling property above, it is enough to generate gamma variables with 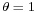 as we can later convert to any value of
as we can later convert to any value of 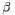 with simple division.
with simple division.
Using the fact that a 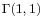 distribution is the same as an
distribution is the same as an 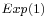 distribution, and noting the method of generating exponential variables, we conclude that if
distribution, and noting the method of generating exponential variables, we conclude that if 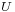 is uniformly distributed on
is uniformly distributed on ![\scriptstyle (0,\, 1]](/2012-wikipedia_en_all_nopic_01_2012/I/45950ff11ee776d6466d25de951484ed.png) , then −
, then −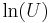 is distributed
is distributed 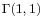 Now, using the "α-addition" property of gamma distribution, we expand this result:
Now, using the "α-addition" property of gamma distribution, we expand this result:
where 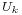 are all uniformly distributed on
are all uniformly distributed on ![\scriptstyle (0,\, 1]](/2012-wikipedia_en_all_nopic_01_2012/I/45950ff11ee776d6466d25de951484ed.png) and independent.
and independent.
All that is left now is to generate a variable distributed as 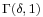 for
for 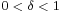 and apply the "α-addition" property once more. This is the most difficult part.
and apply the "α-addition" property once more. This is the most difficult part.
We provide an algorithm without proof. It is an instance of the acceptance-rejection method:
- Let
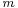 be 1.
be 1. - Generate
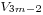 ,
, 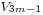 and
and 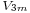 as independent uniformly distributed on
as independent uniformly distributed on ![\scriptstyle (0,\, 1]](/2012-wikipedia_en_all_nopic_01_2012/I/45950ff11ee776d6466d25de951484ed.png) variables.
variables. - If
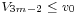 , where
, where 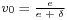 , then go to step 4, else go to step 5.
, then go to step 4, else go to step 5. - Let
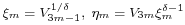 . Go to step 6.
. Go to step 6. - Let
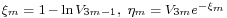 .
. - If
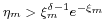 , then increment
, then increment 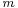 and go to step 2.
and go to step 2. - Assume
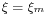 to be the realization of
to be the realization of 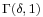 .
.
To summarize,
where
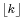 is the integral part of
is the integral part of 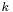 , and
, and 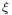 has been generated using the algorithm above with
has been generated using the algorithm above with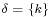 (the fractional part of
(the fractional part of 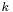 ),
),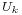 and
and 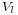 are distributed as explained above and are all independent.
are distributed as explained above and are all independent.
Related distributions
Specializations
- If
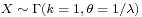 , then X has an exponential distribution with rate parameter λ.
, then X has an exponential distribution with rate parameter λ. - If
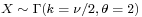 , then X is identical to χ2(ν), the chi-squared distribution with ν degrees of freedom. Conversely, if
, then X is identical to χ2(ν), the chi-squared distribution with ν degrees of freedom. Conversely, if 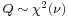 and c is a positive constant, then
and c is a positive constant, then 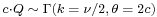 .
. - If
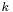 is an integer, the gamma distribution is an Erlang distribution and is the probability distribution of the waiting time until the
is an integer, the gamma distribution is an Erlang distribution and is the probability distribution of the waiting time until the 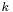 -th "arrival" in a one-dimensional Poisson process with intensity 1/θ. If
-th "arrival" in a one-dimensional Poisson process with intensity 1/θ. If 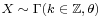 and
and 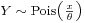 , then
, then 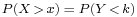 .
. - If X has a Maxwell-Boltzmann distribution with parameter a, then
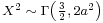 .
. 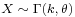 , then
, then 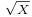 follows a generalized gamma distribution with parameters
follows a generalized gamma distribution with parameters 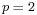 ,
, 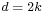 , and
, and 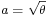 .
.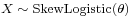 , then
, then 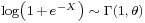 ; i.e. an exponential distribution: see skew-logistic distribution.
; i.e. an exponential distribution: see skew-logistic distribution.
Conjugate prior
In Bayesian inference, the gamma distribution is the conjugate prior to many likelihood distributions: the Poisson, exponential, normal (with known mean), Pareto, gamma with known shape σ, inverse gamma with known shape parameter, and Gompertz with known scale parameter.
The Gamma distribution's conjugate prior is:[5]
Where Z is the normalizing constant, which has no closed form solution. The posterior distribution can be found by updating the parameters as follows.
Where 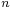 is the number of observations, and
is the number of observations, and 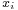 is the
is the 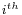 observation.
observation.
Compound gamma
If the shape parameter of the gamma distribution is known, but the inverse-scale parameter is unknown, then a gamma distribution for the inverse-scale forms a conjugate prior. The compound distribution, which results from integrating out the inverse-scale has a closed form solution, known as the compound gamma distribution.[6]
Others
- If X has a Γ(k, θ) distribution, then 1/X has an inverse-gamma distribution with parameters k and θ−1.
- If X and Y are independently distributed Γ(α, θ) and Γ(β, θ) respectively, then X / (X + Y) has a beta distribution with parameters α and β.
- If Xi are independently distributed Γ(αi,θ) respectively, then the vector (X1 / S, ..., Xn / S), where S = X1 + ... + Xn, follows a Dirichlet distribution with parameters α1, …, αn.
- For large k the gamma distribution converges to Gaussian distribution with mean
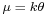 and variance
and variance 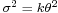 .
. - The Gamma distribution is the conjugate prior for the precision of the normal distribution with known mean.
- The Wishart distribution is a multivariate generalization of the gamma distribution (samples are positive-definite matrices rather than positive real numbers).
- The Gamma distribution is a special case of the generalized gamma distribution.
- Among the discrete distributions, the negative binomial distribution is sometimes considered the discrete analogue of the Gamma distribution
Applications
The gamma distribution has been used to model the size of insurance claims and rainfalls.[7] This means that aggregate insurance claims and the amount of rainfall accumulated in a reservoir are modelled by a gamma process. The gamma distribution is also used to model errors in multi-level Poisson regression models, because the combination of the Poisson distribution and a gamma distribution is a negative binomial distribution.
In neuroscience, the gamma distribution is often used to describe the distribution of inter-spike intervals.[8] Although the gamma distribution often provides phenomenologically a good fit, there is no underlying biophysical motivation of it.
In bacterial gene expression, the copy number of a constitutively expressed protein often follows the gamma distribution, where the scale and shape parameter are, respectively, the mean number of bursts per cell cycle and the mean number of protein molecules produced by a single mRNA during its lifetime.[9]
The gamma distribution is widely used as a conjugate prior in Bayesian statistics. It is the conjugate prior for the precision (i.e. inverse of the variance) of a normal distribution. It is also the conjugate prior for the exponential distribution.
See also
Notes
- ^ See Hogg and Craig (1978, Remark 3.3.1) for an explicit motivation
- ^ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model". Journal of Econometrics (Elsevier): 219–230. http://www.wise.xmu.edu.cn/Master/Download/..%5C..%5CUploadFiles%5Cpaper-masterdownload%5C2009519932327055475115776.pdf. Retrieved 2011-06-02.
- ^ Papoulis, Pillai, Probability, Random Variables, and Stochastic Processes, Fourth Edition
- ^ W.D. Penny, KL-Divergences of Normal, Gamma, Dirichlet, and Wishart densities
- ^ Fink, D. 1995 A Compendium of Conjugate Priors. In progress report: Extension and enhancement of methods for setting data quality objectives. (DOE contract 95‑831).
- ^ Dubey, Satya D. (December 1970). "Compound gamma, beta and F distributions". Metrika 16: 27–31. doi:10.1007/BF02613934. http://www.springerlink.com/content/u750hg4630387205/.
- ^ Aksoy, H. (2000) "Use of Gamma Distribution in Hydrological Analysis", Turk J. Engin Environ Sci, 24, 419 – 428.
- ^ J. G. Robson and J. B. Troy, "Nature of the maintained discharge of Q, X, and Y retinal ganglion cells of the cat," J. Opt. Soc. Am. A 4, 2301-2307 (1987)
- ^ N. Friedman, L. Cai and X. S. Xie (2006) "Linking stochastic dynamics to population distribution: An analytical framework of gene expression," Phys. Rev. Lett. 97, 168302.
References
- R. V. Hogg and A. T. Craig. (1978) Introduction to Mathematical Statistics, 4th edition. New York: Macmillan. (See Section 3.3.)'
- S. C. Choi and R. Wette. (1969) Maximum Likelihood Estimation of the Parameters of the Gamma Distribution and Their Bias, Technometrics, 11(4) 683–690
External links
|
|||||||||||
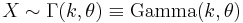
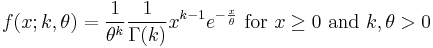
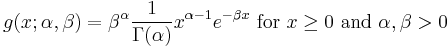
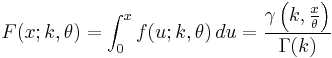
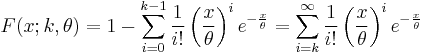
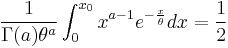
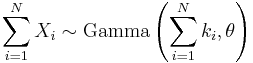
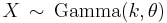
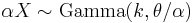
![\begin{align}
& {}\qquad -\frac{1}{\theta^k \Gamma(k)} \int_0^\infty \frac{x^{k-1}}{e^{\frac{x}{\theta}}} \left[ (k-1)\ln x - \frac{x}{\theta} - k \ln\theta - \ln\Gamma(k) \right] \,dx \\[8pt]
& = -\left( [k-1] [\ln\theta %2B \psi(k)] - k - k \ln\theta - \ln\Gamma[k] \right) \\[8pt]
& = k %2B \ln\theta %2B \ln\Gamma(k) %2B (1-k)\psi(k)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/5acc59f6564caa3b1f62209646fc6f26.png)
![\mathbb{E}[\ln(x)] = \psi(k) - \ln(\beta)](/2012-wikipedia_en_all_nopic_01_2012/I/379447ae81736f73345f2948ba9fa565.png)
![\mathbb{E}[\ln(x)] = \psi(k) %2B \ln(\theta)](/2012-wikipedia_en_all_nopic_01_2012/I/e9cc98fe44873780f0e773e569dd464f.png)
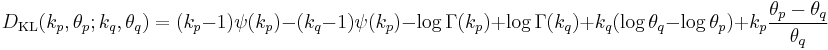
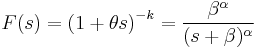
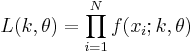
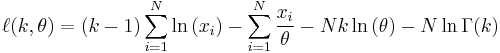
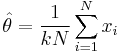
![\ell = (k-1)\sum_{i=1}^N\ln{(x_i)} - Nk - Nk\ln{\left(\frac{\sum x_i}{kN}\right)} - N\ln[\Gamma(k)] \,\!](/2012-wikipedia_en_all_nopic_01_2012/I/4046d02b28223357b50f6adcc891e477.png)
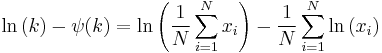
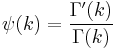
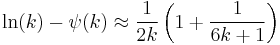
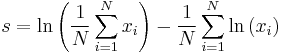
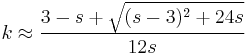
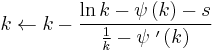
![\psi\left(k\right) = \begin{cases}
\ln(k) - \left( 1 %2B \left[ 1 - \left( 1/10 - 1 / 21k^2 \right) / k^2 \right] / 6k \right) / 2k , \quad k \geq 8 \\
\psi\left( k %2B 1 \right) - 1/k, \quad k < 8
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/a3ff7cb0c7d2b2f04e2d86e54ad301a2.png)
![\psi\;'\left(k\right) = \begin{cases}
( 1 %2B [ 1 %2B ( 1 - [ 1/5 - 1 / 7k^2 ] / k^2 ) / 3k ] / 2k ) / k, \quad k \geq 8, \\
\psi\;'\left( k %2B 1 \right) %2B 1/k^2, \quad k < 8
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/6b38aceb5f47c0c3445cd6fdcd65b84d.png)